金融時系列プライスの予測

もし金融時系列予測の目的を利益の最大化とするならば、この最終結果にむけてNNを調整することが論理的だろう。

例えば、もしこの考えに沿ってトレードを行うのならば、学習サンプルに使われたすべての例により平均化された次の学習エラー汎関数をNN学習のために選択できる。

ここでトレードに使う資金の割合が学習中に調整されるように、ネットワーク出力に追加する形で導入する。

このアプローチのために、最初のニューロン（認識関数or活性化機能をもったもの）は利益率の増加（または減少）の可能性を算出する。

そして２つめのネットワーク出力は資金の推奨された割合を次のトレードで投資する。

しかし先の解析によればこの割合は予測の信用度に比例するため、２つのネットワーク出力をという１つのものに置き換え、そして全体的なパラメーターであるδただ一つを最適化することへと絞ることでエラーは最小化される。

これはネットワークにより予測されるリスクのレベルに比例した投資する資金の割合を調整する機会を生み出す。

そして固定比率で行うよりも多くの利益を生み出す都度変化する比率を使ってトレードを行う。

確かに、もし平均の予測可能性から決定された固定比率を使えば資金成長率はに比例するだろうが、一方で毎回最適化された比率を選択すれば資金成長率はに比例するだろう。

一般的にはシナプス荷重の最初の値がランダムに選択される性質により、同じサンプルでトレーニングを行った異なるネットワークによる予測には、違いが生じる。

この短所（不確実性をもつ要素）を、複数の異なるNNからなるコータリニューラルエキスパートを形成するという長所へと変えることができる。

このエキスパートによる予測のばらつきは、「正しいトレード戦略を選択するために利用できる」予測の信用度に関するアイデアを与えてくれる。

コータリの数値の平均が同じNNで作られたエキスパートの数値の平均よりも優れた予測を出すのは簡単である。

ここで入力値Ｘをもつi 番目のエキスパートのエラーをとする。

コータリのエラーの平均は”コーシーの不等式”の視点で見ると、個々のエキスパートの平均二乗エラーよりも必ず小さくなる。

本質的にエラーが減少することは注目に値する。
もし個々のエキスパートのエラーがお互いに相関がないすなわち

であれば、Ｌ個のエキスパートからなるコータリの平均二乗エラーは１つのエキスパートによるエラーの平均よりも倍も小さいのである。

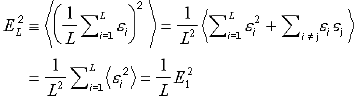
これがなぜすべてのコータリの平均値を元に予測を行うのがいいのかという理由である。
これを図１２に示した。

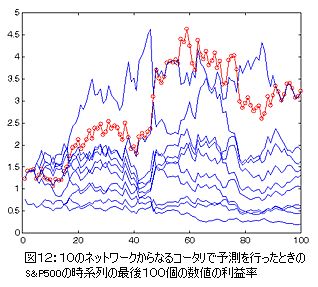
この図で、コータリ（赤い○）による利益率はエキスパートの平均による利益率よりも高いことがわかる。
コータリによる正確に予測されたサインの成績は５９：４１であった。
このケースではコータリによる利益率が各エキスパートのものよりも高い。

このように、コータリを利用する方法は本質的に予測の質を向上させることが可能である。
利益率の値に注目してほしい。
コータリによる資金はマーケットでの１００回の取引で３．２５倍も増加している（もちろん取引にかかるコストを考慮に入れた上での数値である）。

指標の（増分）時系列についての３０個の連続した指数移動平均（EMA1,,,EMA30）から、ネットワークが学習し次の段階での増加のサインを予測する。

この実験では、与えられた予測精度（５９の正確な予測サイン：４１の不正確なサイン）に最適化されたものに近似したレベルに率は固定されている。

つまり、である。
図１３では、同じ予測でよりリスク（正確には　）をとったトレードを行った結果を見ることができる。

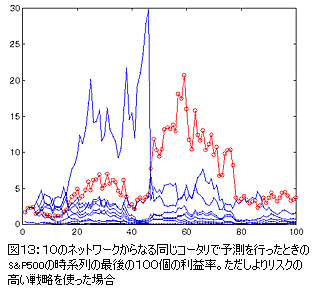
このリスクの数値が前記と同じぐらい最適値に近いため、コータリの利益は同じ（実際はわずかに高い）ままである。

しかしながら大部分のネットワークによる予想は総じてコータリによる予測よりも精度が低く、このような数値は極めてリスクの高いものであり事実上破滅的な結果へとつながる。

上記の例は予測の質の正確な実験が可能であることがいかに大切であり、そしてこの実験が同じ予測において利益率をいかに上げることに使えるのかということを説明している。

我々はより極端な行動に移すことが可能であり、ネットワークの平均の変わりにネットワークの”荷重”オプションを使うことができる。

学習サンプルに対してコータリの予測能力を適応最大化するように荷重を選択しなければならない。
結果として、コータリの下手に学習したネットワークはわずかしか貢献せず、予測を駄目にはしない。

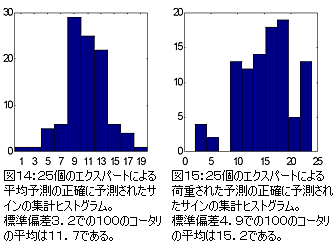
この方法の可能性を次の２つの図１４と１５に２５個のエクスパートからなるコータリネットワーク２種類による予測の比較を表した。

これらの予測は同じ仕組みを使って行われている。
入力として、時系列の指数移動平均を使用し、この平均に使う数はフィボナッチ数列の最初の１０個の数値である。

１００回の実験から得られた結果によれば、荷重予測は（不正確な予測サインを超えた）正確な予測サインの平均過剰を与える。平均予測ではこの値は約１２であるが、荷重予測では約１５である。

この期間内でプライスの減少率と比較したプライスの上昇の総量が１２であることに注目してほしい。

これにより、主な傾向を”＋”のサインの一定の予測として増加するものとみなすことは、正確に予測されたサインの割合が、２５個のエキスパートによる荷重された判定と同じという結果を与える。