時系列データの投入方法
目次
初めに、Ctと定義したプライス（相場時価）自体の値をNNの入力または出力として使用していないことを覚えておいてほしい。
プライスの変化が予測の真のサインとなる。
この変化の値が一般にプライスの値よりもかなり小さいため、（時系列で連続した）プライスの値同士の間には「次の値として最も可能性のあるものはその1つ前の値である」という強い相関関係がある。
これは次の式で表せる。
また同時に学習の質を向上させるためにこれ（＝相関関係？）が繰り返し強調されるため、入力データが統計的に独立しているように（言い換えれば入力データのこのような相関をなくすように）工夫する必要がある。
これが最も統計的に独立した値を入力に選ぶことが論理的であることの理由であり、その値は例えば変化率ΔCや相関増加対数
である。
この相関増加対数は、長期続いている時系列、インフレの影響が極めて著しくなっている（時系列の）部分に適している。
このようなケースではその時系列内の異なる部分どうしでは、その幅が異なるという違いがある。
そのため、これらは実際に異なる単位で測定される。
反対に相場時価間の変化率は測定する単位に関係なく同じ尺度である。（測定の単位はインフレによって変化するが）
結果として時系列のもつ大きな定常性は、我々により長い時系列を（NNに）学習させさらにその学習を向上させることを可能にしている。
遅延空間へ投入することの短所はネットワークの”視野”が限られていることだ。
反対にテクニカル分析は（少し前までの）過去だけでなく（時には）かなり前の時系列の値も分析の対象となる。
例えば時系列の相対的にずいぶんと前の最高値と最安値でさえ、トレーダの心理にかなり強く影響を与えるほどの力をもつ。
そのため、これらの（かなり前の）値は（まだ）予測のためのシグナルとなるに違いない。
遅延空間へ投入するための”窓”の大きさが十分でないものは、このような情報を与えることができず当然予測への影響力は低下する。
その一方で、この”幅”をカバーするような大きさにまで”窓”を広げると、その時系列の極端な値は、ネットワークの次元を増やしてしまう。
このことはNNが大きくなることにより、NNによる予測の精度を下げる結果となる。
この膠着したように思われる状態を脱出する方法は、時系列の過去の動きをコーディングする他の方法である。
より過去へとデータを遡るほど、そのデータの細かい動きは予測結果に影響しなくなることは直感的にわかるだろう。
これはトレーダが過去を主観的に知覚していることによるものであり、厳密言えばこのことが未来を作っている。
そのため、時系列のそのような動きが見られる部分を我々は見つけるべきであり、その精度は選択可能（より過去になるほど詳細はぼける（精度が下がる）。）であろう。
また同時に、（時系列の描く）カーブの全体的な様相は変わらずそのままである。
ここで、いわゆるウェーブレット分解がかなり有望である。
ウェーブレット分解はその情報量が遅延空間投入の方法と同等でありながら、過去の描写精度を調整することでデータを容易に圧縮できる。
入力の次元（属性の数）を減らす
このデータ圧縮は過剰なまでに大きな数の入力変数から予測をするのに最も有効な属性を抽出する例の１つだ。
属性をシステマティックに抽出する方法はすでに前記したとおりである。
これらはまた引き続き時系列の予測へと適用することができる。（されるべきである。）
入力データの表現の仕方がデータ抽出を促進するかもれしないということは重要なことだ。
ウェーブレット分解という表現方法が（属性抽出という観点において）コーディングのいい例である。(Kaiser, 1995）
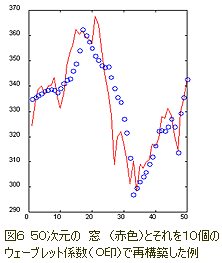
例えば次のグラフ（図６）はある時系列の５０個の数値と、それらを１０個の特別に選んだウェーブレット係数により再構築したものを表している。
このグラフで、再構築にはデータより５倍少ない量を必要とするが、時系列の間近の（再構築した）値が正確に再構築され、より過去になるにつれて高低を正確に反映しながらも大まかなアウトラインとして再構築されていることをよく見てほしい。
よって５０次元の”窓”をたった１０次元の入力ベクターを使って許容レベルの精度で表現することが可能なのである
もう一つの可能なアプローチは、属性の空間として対象となりうるものとして、適切なソフトウェア（MetaStockやウォールストリートのウィンドウのようなもの）で自動的に計算されるさまざまなテクニカル指標を使うことである。
これらのテクニカル指標それぞれを対象となる時系列へ適用した後にそれらが役立つことがたまたまわかるのだが、このような経験に基づいた指標の数の膨大さ（Colby, 1988）はそれらの使用を難しくしている。
つまりこのアプローチは、最も信頼できるテクニカル指標の組合せをNNの入力データとして選ぶという方法である。
手がかりの方法
金融予測の欠点の１つはNN学習の例（サンプル）が不足していることである。
一般的に言えば、金融市場（特にロシア市場）は安定していない。
歴史のまだ浅い市場に新しい指標（インデックス）が現れると、古い市場での取り引きの性質は変化する。
このような状態ではNNに利用可能な時系列の長さは限られている。
しかしながら時系列の動きについての不変式に関するある推測的考えを使って、サンプル例を増やすことができる。
これは物理数理学の技術であり、金融予測の質をかなり向上させる。
その内容は、１つの実際の例にさまざまな加工を行って人工の例（手がかり）を作るというものだ。
このアイデアについて例を挙げて説明しよう。
次に述べる仮定は心理的に納得できることである。
トレーダーがたいてい注目しているのは、プライスが描くチャートの曲線の形であって、そのチャート座標上のプライスの値自体ではない。
だからもし我々がすべての時系列チャートをプライス軸方向に少し拡大すれば、その拡大された時系列をNNの学習に使うことが可能である。
- ＊quotes axisをプライス軸と訳した。”時間軸方向に拡大＝より細かい時間足のチャートにする”というのであればイメージしやすいが、そうはいう意味はない。
このようにしてトレーダーが時系列をどう理解しているのかという心理的特性から生じる推測的情報を使うことによって、サンプル例の数を倍にすることができる。
加えてサンプル例の数を増やすのと並行してその中から解決法を探すために関数のクラスを制限する。
これはまた予測の質を向上させることになる。（当然、使われている不変式が事実に忠実であることが前提である）
S&P500の予測可能性を下図（図７、図８）で見られるボックスカウンティング法によって計算した結果が、手がかりの役割を明らかにしている。
このケースでは属性の空間が直交化法により形成されている。
３０のメインの要素を入力変数として１００次元遅延空間に使用した。
そしてこれらの要素から７つの属性を最も有効な直交線形合成として選択した。
下図からわかるようにこのケースでは、手がかりのアプリケーションのみが目だった予測可能性を与えることができるという結果となった。
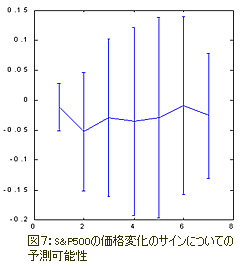
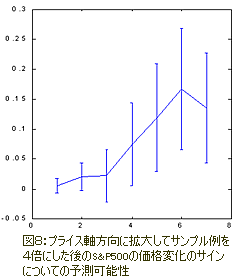
直交空間の使用が標準の投入法と比べて確実に予測可能性が（図５の0.12bitsから図８の0.17bitsに）向上した結果となったことに注目してほしい。
この少し後で利益についての予測可能性の影響について検討するがそのときに、これにより利益率が１．５倍になることを証明する。
これとは別に数は少ないが、解決策を探すためのNNの手引きを上手く使った少ない例がある。
それはＦＸトレードに隠された対称性を使用することだ。
この対称性という観念は、ＦＸのプライスを２つの視点から見ることである。
例を挙げると、ＤＭ（ドイツマルク）／＄として見るのかまたは＄／ＤＭとして見るのか、ということである。
前者が増加すると、後者はそれに合わせて減少する。
この特性はサンプル例の数を２倍にすることに使用できる。
つまり、
のような例にその対称となる
を加えるのである。
NNを使った予測の実験はＦＸ市場においてこの対称性を考えに入れたことで利益率はほぼ倍になった。
もっと正確に言えば、実際の手数料を差し引いても年５％から１０％へと増加した。（Abu-Mostafa, 1995）
予測の質を測定する
金融時系列を予測することはそれ自身を多次元関数の近似という問題へ変換することになるが、NNの入力を形成することと出力を選択することはそれぞれ固有の特徴をもつ。
入力については前記したので、今度は出力変数の選択の特性について研究してみよう。
しかしまず最初に、本来の質問「金融予測の質はどのように測るのか」に答えなければならない。
このことは最適なNN学習戦略を見つけるための手助けとなる。
予測の可能性と利益率の関係
金融時系列予測に特有な性質は最大限に利益を得ることを目標とすることであり、慣例的に関数の近似を行うが平均二乗偏差を最小にすることを目的とすることではない。
デイトレードの最も単純なケースでは、利益はプライスの変化を正確に予測したサインに依存する。
これがなぜNNがプライスの値そのものではなくサインを精密に予測することを目標とするのかという理由である。
それでは毎日マーケットで取引したときの最も単純な結果において、利益率がサインの検出精度とどのような関係にあるのかを見てみよう（図９）。
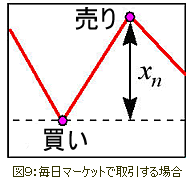
時間ｔにおける投資の全資産をＫｔとすると、相対的なプライスの変化は
であり、そしてNNの出力としてこの変化のサインの信用度
を使うことにする。
形式の非線形出力をもつネットワークは変化のサインを予測する方法を学習し、その予測可能性に比例した範囲でサインを予測する。
そして時間ｔにおける資産売却益は次のように記録される。
ここでδは資産におけるトレードに使う資金の割合（資本分配率）である。
最適な大きさのδを選択してこのＫｔの値を最大にする。
これはトレーダーにサインの
を正確に予測させると共に
の確率で不正確となる。
そして利益率の対数は
となり、利益率自体は
の値が最大値となる時であり、
平均値は
となる。
ここで
の係数を導入する。
例としてガウス分布では
となる。
サインの予測可能性のレベルは直接クロスエントロピーに関係している。このクロスエントロピーはボックスカウンティング法によって推測的に試算されたものである。
バイナリ出力されたものは次のようになる（図１０）。
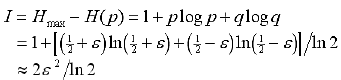
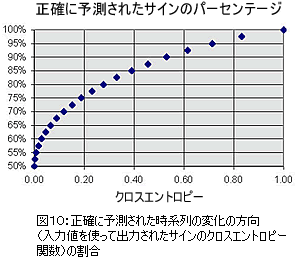
最終的に、サインの予測可能性の値を Ｉ（ビットで表したもの）としたときの利益率の推定として次の式が得られる。
これは Ｉ の予測可能性をもつ時系列にとってマーケットへの
回のエントリーの範囲で資金を倍にすることは原理的に可能であることを意味している。
例を挙げると、明確にS&P500時系列の予測可能性がI = 0.17（図８を参照））と計算された場合、マーケットへ
回のエントリーでは資金を平均２倍に増やせると仮定される。
つまり小さなプライス変化のサインの予測可能性でさえ著しく利益率をあげることができる。
最適な利益率のためにマーケットへかなり注意してエントリーすることが求められ、トレーダーは厳密に決められた（トレードに使用する）資金の割合をリスクにさらすことになる。
すなわち
となる。
ΔK はこのマーケットのボラティリティ
における標準的な利益／損失の大きさであり、この（ΔK）/Kの値が大きくても小さくても利益は減少する。
大変リスクの高いトレードはいかなる予測可能性でも資金を失う可能性がある。
この事実を図11に表した。
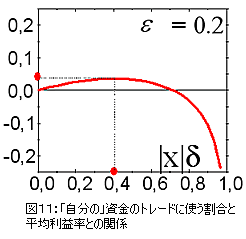
これが、なぜ今まで（上記で）行ってきた実験から利益率の限界のみの実態が伝わってきたのかという理由である。
ゆらぎ効果を考えたより入念な研究はこの記事の範囲を超える。
しかしながら最適なトレード投入資金の大きさの選択には各段階で予測精度の実験が必要となることは定性的に明らかである。