正規分布と比較しない
以上の結果から”「価格変動のボラティリティはその価格に比例する」のか?”
ということについて結論を出したいのだが、正規分布していないため判断ができない。
(解析前の時点では正規分布していればこの説は成り立ち、いびつな分布であれば成立しない、と考えていた)
すでに書いたがボラティリティの計算が
ボラティリティ=「(高値ー安値)÷始値」の1000倍
であり、(高値ー安値)と 始値(価格)は0以上の値となる。
これによりボラティリティが常に0以上であることが正規分布しない理由だ。
正規分布と比較すること自体間違っていたのである。
このように値が常に0以上である場合の分布、例えば金融や個体数などの統計では実は対数正規分布が使われることが多い(ことがわかった)。
http://www1.parkcity.ne.jp/yone/math/mathB03_08.htm
http://aoki2.si.gunma-u.ac.jp/lecture/Bunpu/log-normal.html
対数正規分布の説明は、この2つのページが少しばかりは参考になる。
つまりボラティリティの分布図を正規分布図と比較したいのであればボラティリティの対数の分布図を作成する必要がある。
「じゃあ今まで長い無駄な話を読まされていたのか。」と不快になる人もいるかもしれないが、そこはご勘弁を。
これがまさに試行錯誤というもので、このことを知っていなかったため、少し遠回りをしましたが、誤りに気づき正しい道にもどってきましたので、、、、。
そこでボラティリティの計算のプログラム 06_Calc_Vola_Eachstock.exe を加工して、ボラティリティの対数とその分布についての計算もできるように変更した。
Caliculate のボタンの横にある Ln Vol にチェックを入れることで可能となる。
ただしボラティリティが0であるときの対数は(計算できないため、ボラティリティを0.01としたときの対数の)近似値-5とした。
また対数は自然対数を使用した。
比較しやすいように、加工前のボラティリティについての標準偏差・歪度・尖度のヒストグラムを載せる。
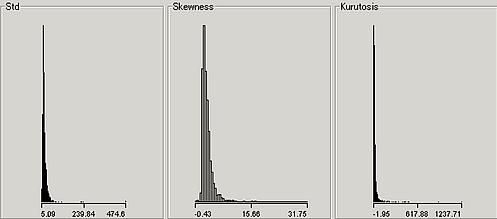
ボラティリティのヒストグラム
ボラティリティの対数のヒストグラム
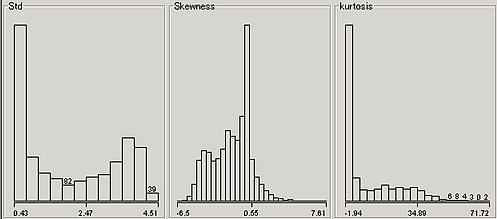
ボラティリティの自然対数をとった結果、ヒストグラムはご覧の通りいびつになってしまった。
原因は、ボラティリティが0のときに対数を-5としたことであると思われる。
それならば、ボラティリティが0のレコードをデータに含めない場合はどうなるか。
いびつさは解消されないだろうか。
プログラムを加工し、ボラティリティが0の場合は無視できるようにし、再び計算した。
(Caliculate のボタンの横にある Ignore Vol 0 にチェックを入れることでこの計算が可能となる。
この場合は、 Ln Vol と Ignore Vol 0 の2つにチェックを入れてからCaliculateのボタンを押す。)
この結果は次の通り。
ボラティリティの対数のヒストグラム、ボラティリティが0のレコードは省いたもの
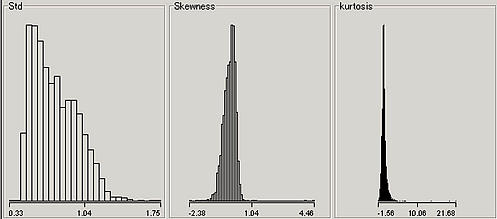
結果は改善されたように思える。しかしこれは”改善したかのように見えるように加工した”と言える。
ボラティリティが0のレコードを省く以外の方法はないのか。
ここで再びボラティリティの計算式について考えてみると、計算の元になる値”価格”自体、0以下になることはない。
そこで対数をボラティリティに対してではなく価格に対して計算することにした。
その場合の(価格の対数を使った)ボラティリティの計算式は
ボラティリティ=「(Ln高値 - Ln安値)÷Ln始値」の1000倍
となる。
再びプログラムを加工し、計算を行わせた。
(Caliculate のボタンの横にある Ln Price にチェックを入れて計算させる。)
価格の対数を使った場合のボラティリティのヒストグラム
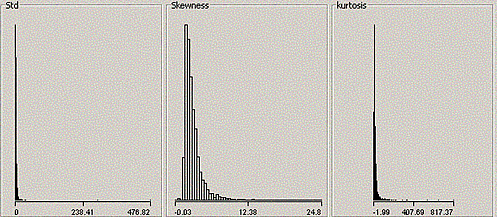
結果は元のボラティリティのヒストグラムと似たものとなった。
それならば今度はボラティリティが0のレコードを省くのではなく、ボラティリティが0のレコードをもつ銘柄を除くのはどうか。
こうすれば、ボラティリティが0のレコードを1つももたない銘柄の統計をとることになる。
07_Export_Data_from_CSV.exe を使って
Number : 3, Condition : If value is , Value : 0
の条件でExportを実施した。
これはボラティリティが0のレコードが1つもないレコードを抽出することを意味する。
価格の対数を使った時のボラティリティのヒストグラムでボラティリティが0の銘柄を含まないもの
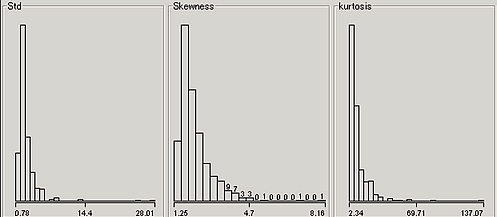
対数分布のような形状は変わらない。
では、3つ前の「ボラティリティの対数のヒストグラム、ボラティリティが0のものは省いたもの」について、ボラティリティが0のレコードをもつ銘柄を除けばどうか。
再び07_Export_Data_from_CSV.exe をさきほどと同じ条件で使った。
ボラティリティの対数のヒストグラム、ボラティリティが0の銘柄は省いたもの
ようやく念願?の正規分布に近づいたヒストグラムを得ることができた。
この時点での銘柄数は480である。
歪度、尖度については0がほぼ最頻値である。
visualizeの次の関係図からも尖度と歪度が0を含むエリアに分布が密集している。
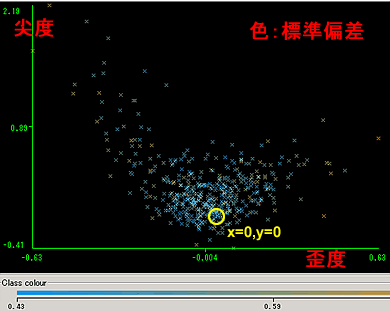
それでは本題の「価格変動のボラティリティはその価格に比例する」という説の検証の結果だが、上図からもわかるが、各銘柄のボラティリティの分布(ヒストグラム)の状態は決して1つにまとまってはいない。
これは自分に向けての注意でもあるが、決して正規分布となるのが正しいわけではない。
データが示す分布それ自体は正しいのであり、それから得られる統計の結果はそのままとらえるものなのだ。
この結果を素直に見れば、「取引の活発な銘柄について、そのような性質をもつ銘柄は100以上存在するが、全般についてはいえない。」というところだろう