ボラティリティとデータ日数の関係、そして尖度と歪度のヒストグラム、国内マーケットデータのデータマイニングの結果から見えてきた結論とは。
ボラティリティとデータ日数の関係を見る
目的はWEKAで見た分布図(ヒストグラム)をより詳細に見ることである。
前記したプログラムを使えば例外的な値のサンプルを、尖度(kurtosis)と歪度(skewness)のそれぞれについて除外すれば、この目的を達成することができる。
しかしその前に、以前書いた”国内マーケットデータのクレンジング”の中で「取引日数が少ない=日の浅い銘柄」の除外を検討したことについて思い出してほしい。
これは日数の少なさとはサンプル数の少なさであり、これがデータマイニング・解析において信頼度の低下につながる。
またそのような条件の銘柄はトレードが行える機会が少ないことも意味する。
そこで先に取引日数の少ない銘柄の除外について検討する。
データを解析して「取引日数とボラティリティの計算結果との間になんらかの関係がある」のがはっきりすれば、この除外が有効であることが実際に示されることになる。
そのためにCalcResult.csvを再びWEKAで開き、尖度・歪度・標準偏差のそれぞれと取引日数との関係図を見ることにする。
Weka Explorer で CalcResult.csv を開き、Visualize のタブをクリックする。
すると各フィールド同士の関係図が見える。
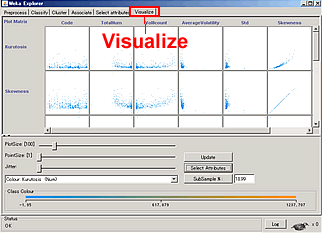
見たい関係図をクリックするとその図が拡大され別ウィンドウで見ることができる。
実はこの関係図は2次元ではなく3次元、つまり3つのフィールドの関係図である。
横軸がX、縦軸がY、色がZとなる。
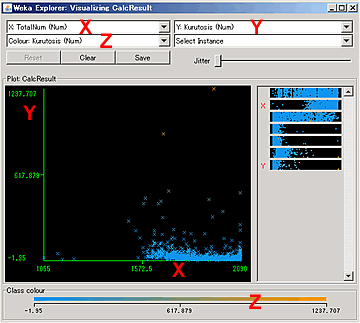
今はX(取引日数)とY(尖度、歪度、標準偏差)についてだけ見ることにする。
取引日数と尖度の関係図
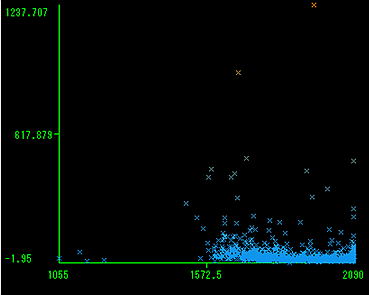
取引日数と歪度の関係図
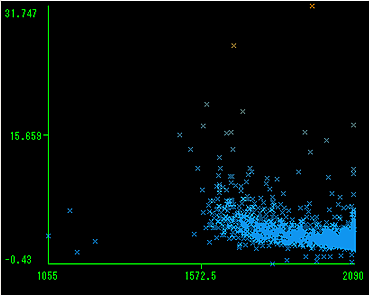
取引日数と標準偏差の関係図
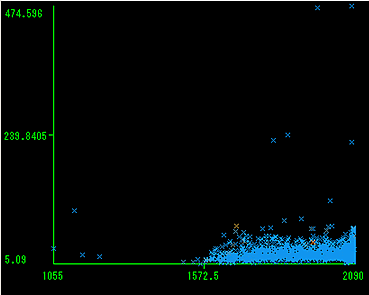
取引日数と歪度の関係図からは、取引日数が少ないと歪度が上昇する傾向が見られ、歪度のヒストグラムが取引日数により影響を受けていることがわかる。
また図からは取引日数が1572未満となる銘柄がかなり少ないことがわかる。
他にも考えられることはないだろうか?
ここで取引日数についてどうカウントしているのかを振り返ると、05_Choose_stocks_by_Index.exe を使って作成された各銘柄の一定期間データのCSVファイル内の行数(レコード数)そのものが取引日数となる。
取引量の大小に関係なくデータとして存在すればカウントされたものである。
取引日数が十分あっても実際に取引が活発でなければ、ボラティリティの計算結果の信頼性も下がるし、トレードの対象からは外したい銘柄となるだろう。
【国内マーケットデータのクレンジング】で、
”「流通量が少ない、取引の少ない銘柄」は出来高や高値と安値の幅などで判断できるかもしれないが、現時点ではその基準がないため、削除できない。”
と述べたが、ここで 高値=安値 のレコードを取引の少ない(ボラティリティ0の)銘柄と考える。
その数を「Vol0count」というフィールドとして算出するが、実はこれも 06_Calc_Vola_Eachstock.exe で算出されている。
それではボラティリティ0の日数(横軸)と尖度・歪度・標準偏差(縦軸)の関係図を見てみる。
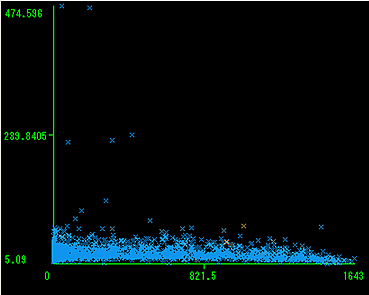
ボラティリティ0の日数と尖度の関係図
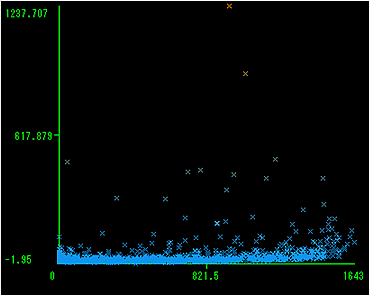
ボラティリティ0の日数と歪度の関係図
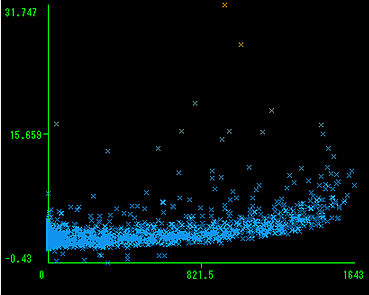
ボラティリティ0の日数と標準偏差の関係図
図から、ボラティリティ0の日数が多いほど尖度と歪度は上昇する傾向があり標準偏差は分布が収束する傾向にあるといえるのだろう。
そして尖度・歪度のヒストグラムはボラティリティ0の日数が多いものによりその分布が影響を受けているとも見ることができるだろう。
ついでにボラティリティ0の日数(横軸)とボラティリティ平均(縦軸)の関係図も見てみる。
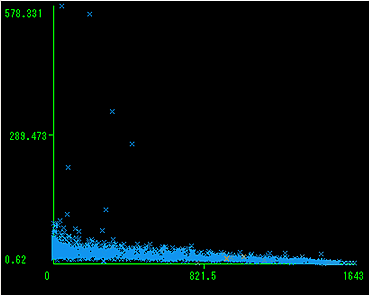
ボラティリティ0の日数が多いほどボラティリティは減少する方向に収束している。
これは先の”「高値ー安値=0」 のレコードを取引の少ない(ボラティリティ0の)銘柄と考える。”はほぼ当たっているといえそうだ。
さらにボラティリティ0の日数(横軸)とトレード日数(縦軸)の関係図も見てみる。
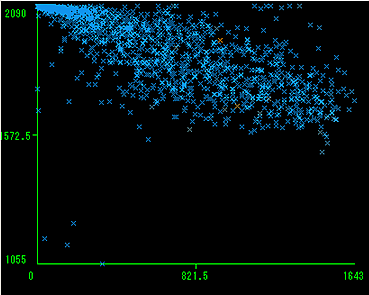
この図からは、当然の話だがボラティリティ0の日数が少ないほど取引の日数(データ日数)は多くなるといえる。
しかしボラティリティ0の日数が多くなるほど、データ日数が少なくなる傾向はあるもののばらつきが多い。
以上から歪度に関してはボラティリティ0の日数とデータ日数がヒストグラムに影響を与えていると考えられ、この2つのフィールドに関して絞込みを行うことにする。
データ日数については、取引日数と歪度の関係図から、明確な基準はないが分布の拡散と歪度の上昇傾向の強まっている境界を目視で判断し、1850以上という条件とする。
取引日数と尖度の関係図と境界
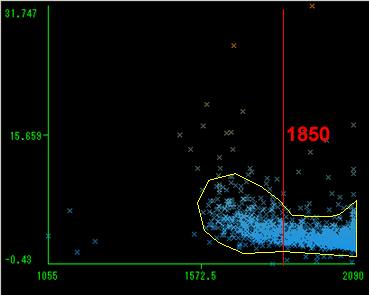
ボラティリティ0の日数についても同様に、ボラティリティ0の日数と歪度の関係図から635以下という条件とする。
ボラティリティ0の日数と歪度の関係図と境界
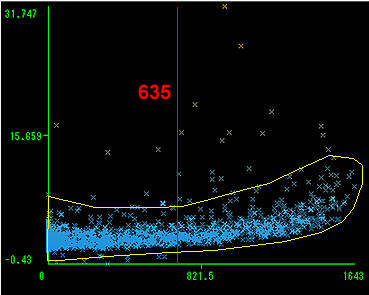
絞込みの条件が決まったため、次はプログラムで抽出を行う。
概要は次のとおり。
07_Export_Data_from_CSV.exe でCalcResult.csvについて
Number : 2, Condition : If value >= , Value : 1850
の条件でExportを実施。
これにより2Over1850_CalcResult.csvとUn_2Over1850_CalcResult.csvが作成される。
つぎに2Over1850_CalcResult.csvについて
Number : 3, Condition : If value <= , Value : 635 の条件でExportを実施。 作成された3Less635_2Over1850_CalcResult.csv をWEKAで開く。