ニュージーランドの無料のデータマイニングソフト「WEKA」を使って国内マーケットのボラティリティについて調べてみたプロセスを詳しく紹介。
手順
目次
WEKAでCSVファイルを開く
今回WEKAはバージョン3.4.12をPCにあらかじめインストールしたものを使う。
Windowsで
スタート > プログラム > WEKA3.4.12 > WEKA3.4 と選択し起動する。
Weka GUI Chooserのウィンドウが現れたら、 Explorer のボタンをクリックする。

Weka Explorerのウィンドウが現れる。
Preprocessタブの中のOpen file.. のボタンをクリックする。
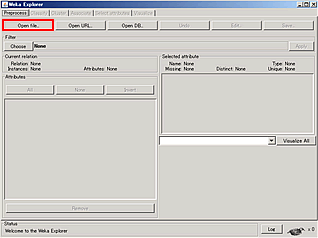
CalcResult.csvのあるフォルダを選択し、ファイルタイプで csv data files を選ぶとCSVファイルが選択できるようになる。
CalcResult.csv を選択し” 開く ”のボタンをクリックする。
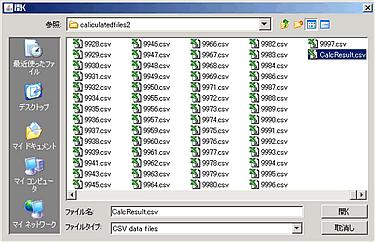
Weka Explorer のウィンドウ下半分にファイル内容が表示されれば成功。
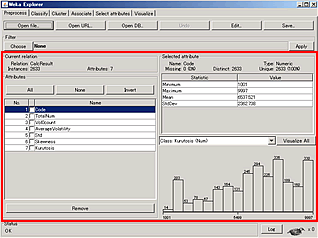
WEKAで分布図(ヒストグラム)を見る
Open file…でファイルを開くことに成功した時点で1個目のフィールドについての分布図(ヒストグラム)がWeka Explorerのウィンドウの右下に自動で表示される。
ヒストグラム左にあるAttributesで表示したいフィールドを選択することができる。
紺色に反転しているフィールドが現在表示されているヒストグラムとなる。
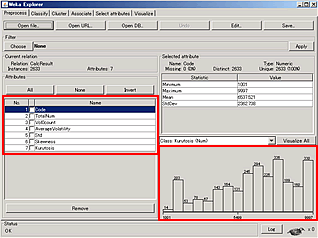
すべてのフィールドのヒストグラムを一度にみたい場合はヒストグラムの上にある Visualize All のボタンをクリックする。
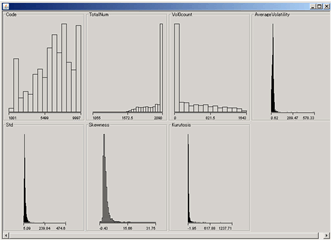
ボラティリティの分布図(ヒストグラム)について考える
いよいよデータマイニング、ということではなくこのWEKAの分布図(ヒストグラム)から考察する。
必要なヒストグラムは尖度、歪度、標準偏差の順の3つである。
ここで復習すると、国内マーケットの各銘柄の日足データについて、(高値ー安値)÷始値の計算結果を1000倍したものをボラティリティとし、ボラティリティが2000年以降どのように分布しているのかを標準偏差・尖度・歪度として計算した。
これをすべての銘柄について算出し、その結果がどのように分布しているのかを表しているのが、今WEKAで表示しているヒストグラムである。
もしどの銘柄もほぼ同じ分布をとるならば、WEKAの標準偏差、尖度、歪度についてのヒストグラムはどれも幅の狭いとがった山状となることが予想できる。
そして各銘柄のヒストグラムが正規分布に近いならば、尖度と歪度は0に近い値となるはずである。
WEKAによる尖度・歪度・標準偏差のヒストグラムを見てみる。
国内マーケットデータのボラティリティの尖度(kurtosis)のヒストグラム
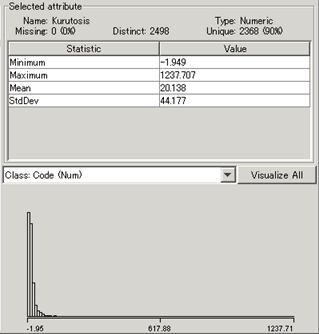
ヒストグラムの上にカーソルをもってくると、その座標とサンプル数が表示される。
ヒストグラムは 最小値-1.949を頂点とし、正の方向に裾が延びている。
最大値は1237.71だが、このあたりは1サンプルしかない。
このような例外値を取り除き、-1.95から75の範囲を拡大して見てみたいがWEKAでは簡単にできないようだ。
これについては後で方法を考える。
頂点は-1.949であるが、その右の棒グラフの値は9.219であるから、頂点はほぼ0といえるかもしれない。
尖度は分布図のとがり具合であるから、尖りは正規分布と比べて、ほぼ同じかもしくは尖りが急で裾が長い形をしていることを意味している。
国内マーケットデータのボラティリティの歪度(skewness)のヒストグラム
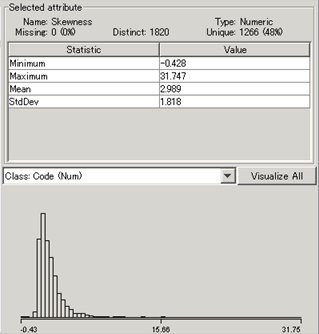
ヒストグラムは 1.87を頂点とし、正の方向に裾が延びている。
最大値は31.747だが、このあたりは1サンプルしかない。
尖度のヒストグラムの場合と同じく、このような値を例外とし、ヒストグラムの中心を拡大して観察したいところだ。
大半が正の値をとっており、これは分布の頂点が左にずれて裾が右に伸びていることを意味している。
尖度と歪度のヒストグラムから正規分布とは違う非線対称の分布をしていることがわかるため、標準偏差の値について調べてもあまり意味がないと判断できるが、一応標準偏差についてのヒストグラムも表示する。
国内マーケットデータのボラティリティの標準偏差のヒストグラム
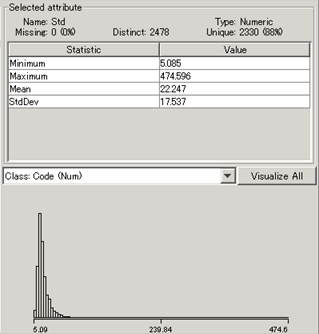
なぜボラティリティが頂点が左にずれて右裾がのびた分布をするのかを考えてみると、ボラティリティの計算式に理由がある。
ボラティリティ=「(高値ー安値)÷始値」の1000倍
この計算からはつねにボラティリティは0以上の値となる。
そのため線対称の分布図とはならず、正の方向のみに裾がのびる。
これで「歪度>=0」の理由もわかった。
次に尖度についてだが、これは普段は正規分布のようなばらつきでボラティリティは変化しているが突如として例外的に大きくなる日が時に発生することを示しているのではないだろうか。